最长回文子串&最长子串&第K大的数字&atoi

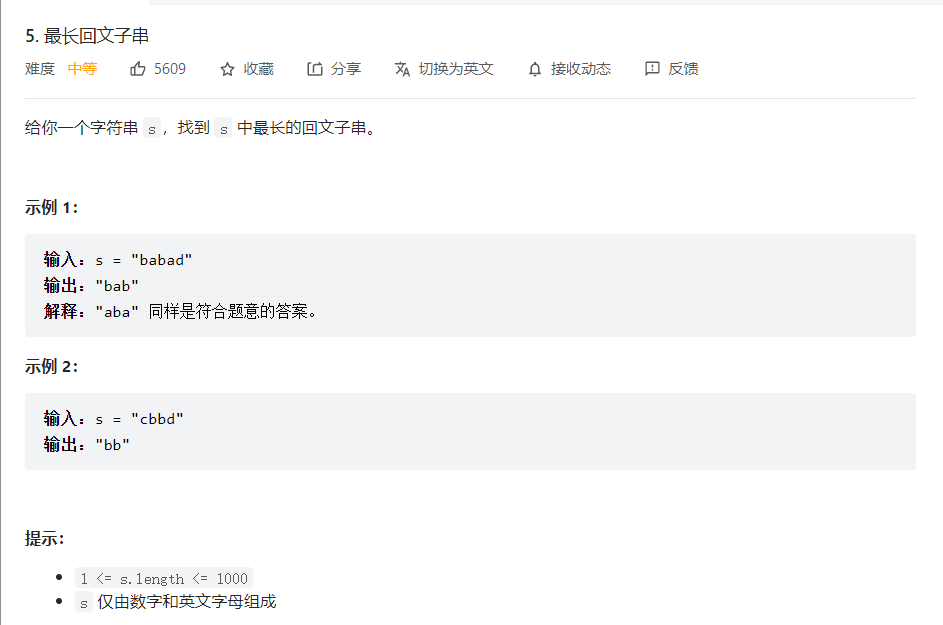
最长回文子串

解题思路：中心扩散法

中心扩散法

其实，我们知道，对于回文子串来说，是对称的。也就是说，从中心开始，往左扩散，往右扩散，一直去比较左右两边，如果一样，就再去往左扩散，往后扩散，直到结束，如果出现不相等的情况，那就说明不是回文子串。我们来举个例子：

接下来的问题是：怎么用代码去实现这个过程。

代码实现

我们遍历这个字符串的每一个字符，第一步，先找到上面的中间相同的a，先往左边找，看看有没有相同的，有的话就往左扩散，找到不相同的或者尽头，同理往右边扩散。第二步就是往左右两边同时对比是否相同：

char * longestPalindrome(char * s){
    int len = strlen(s);
    if(len==0)
    {
         return NULL;
    }
    //最大长度
    int maxLenth = 1;
    //起始下标
    int maxIndex = 0;
    for(int i = 0;i<len;i++)
    {
        //当前位置
        int curIndex = i;
        //左边
        int left = i;
        //右边
        int right = i;
        while(left!=0)
        {
            //相同往左边扩散
            if(s[left-1]==s[curIndex])
            {
                --left;
            }
            else
            {
                break;
            }
        }
        while(right!=len-1)
        {
            //相同往右边扩散
            if(s[right+1] == s[curIndex])
            {
                right++;
            }
            else
            {
                break;
            }
        }
        //往左右两边扩散
        while(left!=0&&right!=len-1)
        {
            if(s[left-1]==s[right+1])
            {
                left--;
                right++;
            }
            else
            {
                break;
            }
        }
        //更新变量
        if((right-left+1)>maxLenth)
        {
            maxLenth = right-left+1;
            maxIndex = left;
        }
    }
    char*str = (char*)malloc(sizeof(char)*(maxLenth+1));
    if(NULL == str)
    {
        return;
    }
    int j = 0;
    for(int i = maxIndex;i<=maxIndex+maxLenth-1;i++)
    {
        str[j++] = s[i];
    }
    str[j] = '\0';
    return str;
}

至此，我们顺利通过了这道题。

无重复字符的最长子串

这道题可以用数组哈希和滑动来进行解决。

定义left和right（初始化为0）这两个变量来记录左右的边界，让字符串中的每一个元素作为数组hash（初始化为0）的下标，我们以s[right]作为判断的条件，第一次出现就hash[s[right]]++，同时右边界往右走，既right++,如果出现重复，此时的hash对应的下标已经不是0了，我们就hash[s[left]]–,同时左边界left也要进行更新，left++.

定义count去记录right-left的最大值。接下来就是代码的实现了：

int lengthOfLongestSubstring(char * s){
    char hash[128];
    memset(hash,0,sizeof(hash));
    int left = 0,right = 0,count = 0;
    while(s[right])
    {
        if(hash[s[right]])
        {
            hash[s[left]]--;
            ++left;
        }
        else
        {
            hash[s[right]]++;
            ++right;
        }
        //更新count
        count  =count<(right-left)?(right-left):count;
    }
    return count;
}

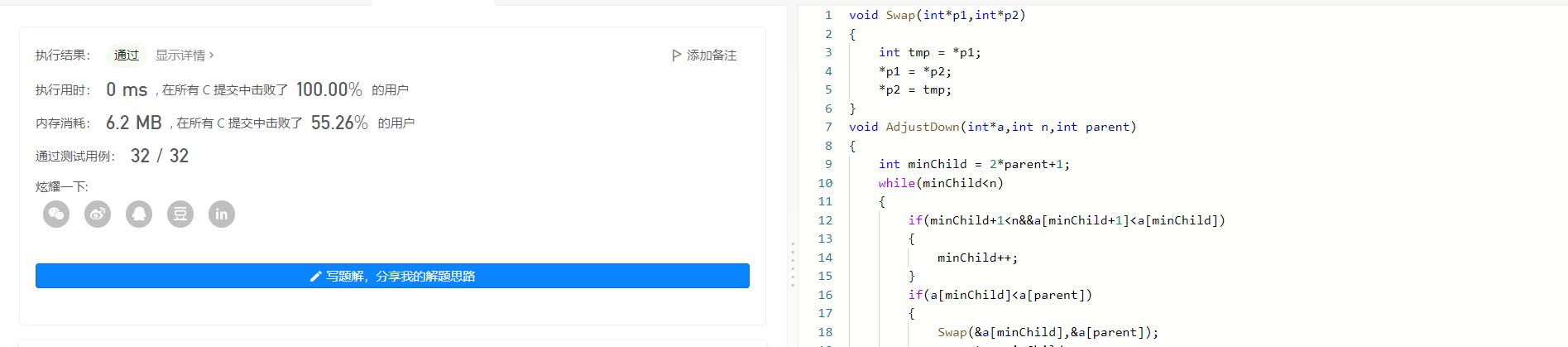
数组中的第 k 大的数字

解题思路：利用堆的应用，topK问题。

题目是要找数组的第K大的数字，我们利用K个数建成一个小堆（向下调整算法）。剩下的数N-k个数我们去和堆顶进行比较，因为是要找第K大的数字，如果比堆顶大，我们就把堆顶替换，同时进行向下调整，最终堆顶就是第K大的数。

void Swap(int*p1,int*p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}
void AdjustDown(int*a,int n,int parent)
{
    int minChild = 2*parent+1;
    while(minChild<n)
    {
        if(minChild+1<n&&a[minChild+1]<a[minChild])
        {
            minChild++;
        }
        if(a[minChild]<a[parent])
        {
            Swap(&a[minChild],&a[parent]);
            parent = minChild;
            minChild = 2*parent+1;
        }
        else
        {
            break;
        }
    }
}

int findKthLargest(int* nums, int numsSize, int k){
    int* minHeap = (int*)malloc(sizeof(int)*k);
    if(minHeap == NULL)
    {
        exit(-1);
    } 
    else
    {
        for(int i = 0;i<k;i++)
        {
            minHeap[i] = nums[i];
        }
        for(int j = (k-1-1)/2;j>=0;j--)
        {
            AdjustDown(minHeap,k,j);
        }
        for(int i = k;i<numsSize;i++)
        {
            if(nums[i]>minHeap[0])
           {
              minHeap[0] = nums[i];
              AdjustDown(minHeap,k,0);
           }
        }
    }
    int ret = minHeap[0];
    free(minHeap);
    return ret;
}

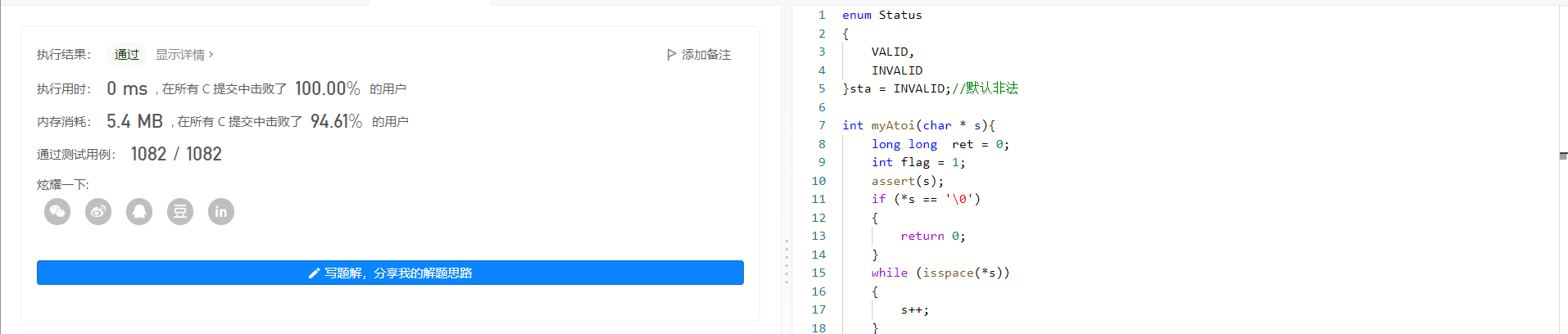
字符串转换整数 (atoi)

一个非常有意思的题目，说难并不算难，但是要求还是蛮多的，注意看要求写代码就行了：

enum Status
{
	VALID,
	INVALID
}sta = INVALID;//默认非法

int myAtoi(char * s){
    long long  ret = 0;
	int flag = 1;
	assert(s);
	if (*s == '\0')
	{
		return 0;
	}
	while (isspace(*s))
	{
		s++;
	}
	if (*s == '+')
	{
		flag = 1;
		s++;
	}
	else if (*s == '-')
	{
		flag = -1;
		s++;
	}
	while (*s)
	{
		if (isdigit(*s))
		{
			//越界
			ret = ret * 10 + flag * (*s - '0');
			if (ret > INT_MAX)
			{
				return INT_MAX;
			}
            if(ret<INT_MIN)
            {
                return INT_MIN;
            }
		}
		else
		{
			return (int)ret;
		}
		s++;
	}
	if (*s == '\0')
	{
		sta = VALID;
	}
	return (int)ret;

}